Answer:
The calculated 99% confidence interval is wider than the 95% confidence interval.
Explanation:
We are given the following in the question:
95% confidence interval for the population proportion
(0.65, 0.69)
Let
 be the sample proportion
be the sample proportion
Confidence interval:
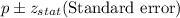

Let x be the standard error, then, we can write
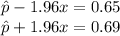
Solving the two equations, we get,
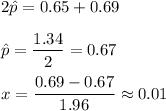
99% Confidence interval:
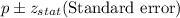
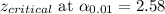
Putting values, we get,

Thus, the calculated 99% confidence interval is wider than the 95% confidence interval .