The length of the rectangle is 11 units
The width of the rectangle is 5 units.
Step-by-step explanation:
The equation of the trinomial is
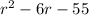
We need to find the length and the width of the rectangle.
The length and width of the rectangle can be determined by factoring the trinomial
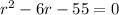
Factoring using the quadratic formula, we have,
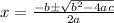
where
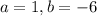 and
and
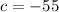
Substituting these in the above formula, we have,
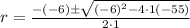
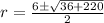
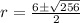
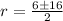
Hence, the two roots of the trinomial are
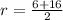 and
and
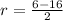
Solving
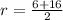 , we get,
, we get,
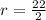
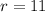
Solving
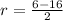 , we get,
, we get,

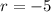
Thus, the solutions of the trinomial are 11 and -5
Since, the length of the rectangle is larger than the width, the length of the rectangle is 11 units.
Also, the width of the rectangle cannot be negative.
Thus, ignoring the negative sign, we have,

Hence, the width of the rectangle is 5 units.