Question

If the standard deviation of a set of data is zero, what can you conclude about the set of values? The sum of the deviations from the mean is zero. All values are identical. All values are equal to zero. The sum of the values is zero

Answer 1

All values are identical.

Explanation:

We are given the following in the question:

If the standard deviation of a set of data is zero.

Then, all the values in data are identical.

This can be shown as:

Let all the terms in data be x.

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n}}`

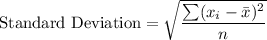
where
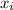`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(nx)/(n) = x`

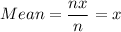
Sum of squares of differences =

`\displaystyle\sum (x_i - x)^2 = 0`

`\sigma = \sqrt{(0)/(n)} = 0`

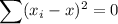
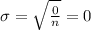
Thus, the correct answer is

All values are identical.