Question

At the bottom of its path, the ball strikes a 2.30 kg steel block initially at rest on a frictionless surface. The collision is elastic. Find (a) the speed of the ball and (b) the speed of the block, both just after the collision.

Answer 1

(a). The speed of the ball after collision is 2.01 m/s.

(b). The speed of the block after collision 1.11 m/s.

Step-by-step explanation:

Suppose, A steel ball of mass 0.500 kg is fastened to a cord that is 50.0 cm long and fixed at the far end. The ball is then released when the cord is horizontal.

Given that,

Mass of steel block = 2.30 kg

Mass of ball = 0.500 kg

Length of cord = 50.0 cm

We need to calculate the initial speed of the ball

Using conservation of energy

`(1)/(2)mv^2=mgl`

`v=√(2gl)`

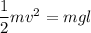
Put the value into the formula

`u=\sqrt{2*9.8*50.0*10^(-2)}`

`u=3.13\ m/s`

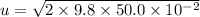
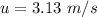
The initial speed of the ball
`u_(1)=3.13\ m/s`

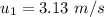
The initial speed of the block
`u_(2)=0`

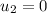
(a). We need to calculate the speed of the ball after collision

Using formula of collision

`v_(1)=((m_(1)-m_(2))/(m_(1)+m_(2)))u_(1)+((2m_(2))/(m_(1)+m_(2)))u_(2)`

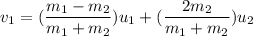
Put the value into the formula

`v_(1)=((0.5-2.30)/(0.5+2.30))*3.13`

`v_(1)=-2.01\ m/s`

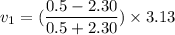
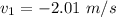
Negative sign shows the opposite direction of initial direction.

(b). We need to calculate the speed of the block after collision

Using formula of collision

`v_(2)=((2m_(1))/(m_(1)+m_(2)))u_(1)+((m_(1)-m_(2))/(m_(1)+m_(2)))u_(2)`

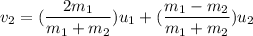
Put the value into the formula

`v_(2)=((2*0.5)/(0.5+2.30))*3.13+0`

`v_(2)=1.11\ m/s`

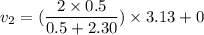
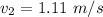
Hence, (a). The speed of the ball after collision is 2.01 m/s.

(b). The speed of the block after collision 1.11 m/s.