Question

In a certain city, the daily consumption of electric power, in millions of kilowatt-hours, is a random

variable X having a gamma distribution with mean
\mu=6 and variance \sigma^{2}=12.
(a) Find the values of \alpha and \beta.
(b) Find the probability that on any given day the daily
power consumption will exceed 12 million kilowatthours.

Answer 1

a)
`\alpha = 3, \beta = 2`

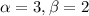
b) 0.0620

Explanation:

We are given the following in the question:

Population mean,
`\mu` = 6

Variance,
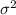`\sigma^2` = 12

a) Value of
`\alpha, \beta`

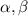
We know that

`\alpha \beta = \mu = 6\\\alpha \beta^2 = \sigma^2 = 12`

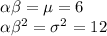
Dividing the two equations, we get,

`(\alpha\beta^2)/(\alpha\beta) = (12)/(6)\\\\\Rightarrow \beta = 2\\\alpha \beta = 6\\\Rightarrow \alpha = 3`

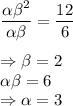
b) probability that on any given day the daily power consumption will exceed 12 million kilowatt hours.

We can write the probability density function as:

`f(x,3,2) = (1)/(2^(3)(3-1)!)x^(3-1)e^{-(x)/(2)}, x > 0\\\\f(x,3,2) = (1)/(16)x^(2)e^{-(x)/(2)}, x > 0`

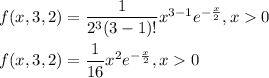
We have to evaluate:

`P(x >12)\\\\= (1)/(16)\displaystyle\int^(\infty)_(12)f(x)dx\\\\=(1)/(16)\bigg[-2x^2e^{-(x)/(2)}-2\displaystyle\int xe^{-(x)/(2)}dx}\bigg]^(\infty)_(12)\\\\=(1)/(8)\bigg[x^2e^{-(x)/(2)}+4xe^{-(x)/(2)}+8e^{-(x)/(2)}\bigg]^(\infty)_(12)\\\\=(1)/(8)\bigg[(\infty)^2e^{-(\infty)/(2)}+4(\infty)e^{-(\infty)/(2)}+8e^{-(\infty)/(2)} -( (12)^2e^{-(12)/(2)}+4(12)e^{-(12)/(2)}+8e^{-(12)/(2)})\bigg]\\\\=0.0620`

0.0620 is the required probability that on any given day the daily power consumption will exceed 12 million kilowatt hours.