Question

wo hydraulic cylinders are connected at their piston ends (cap ends rather than rod ends) by a single pipe. Cylinder A has a 2-in diameter and cylinder B has a 4-in diameter. A 500-lb retraction force is applied to the piston rod of cylinder A. Determine the Pressure at cylinder A. Pressure at cylinder B. Pressure in the connection pipe. Output force of cylinder

Answer 1

1)
`1.10\cdot 10^6 Pa`

2)
`1.10\cdot 10^6 Pa`

3)
`1.10\cdot 10^6 Pa`

4) 2000 lb

Step-by-step explanation:

1)

Pressure is defined as the ratio between the force applied on a surface and the area of the surface:

`p=(F)/(A)`

where

F is the force applied

A is the area of the surface

In this problem, we want to find the pressure at cylinder A.

We know that:

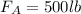`F_A=500 lb` is the force on A, converting into Newtons:

`F_A=500\cdot 4.45 =2225 N`

The diameter of the piston is
`d_A=2 in`, so the radius is

`r_A=1 in = 2.54 cm =0.0254 m`

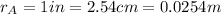
Therefore the area is

`A_A=\pi r_A^2=\pi (0.0254)^2=2.03\cdot 10^(-3)m^2`

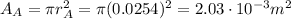
Therefore, the pressure on cylinder A is

`p_A=(2225 N)/(2.03\cdot 10^(-3))=1.10\cdot 10^6 Pa`

2)

We can solve this part by applying Pascal's principle.

In fact, Pascal's principle states that the pressure in a fluid transmits equally over all parts of the fluid.

Therefore in this case, since the two cylinders are connected by a single pipe with a fluid, it means that the pressure on the cylinder A is transmitted equally to the cylinder B.

Therefore, since the pressure in cylinder A was

`p_A=1.10\cdot 10^6 Pa`

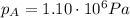
It means that the pressure on cylinder B will be identical:

`p_B=1.10\cdot 10^6 Pa`

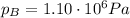
3)

This part is identical to part 2): in fact, as we stated previously, according to Pascal's principle the pressure is transmitted equally to every part of the fluid: therefore in this case, the pressure in the connection pipe is the same as the pressure on cylinder A and B,

`p=1.10\cdot 10^6 Pa`

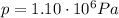
4)

The pressure exerted on cylinder B is given by

`p_B=(F_B)/(A_B)`

where

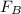`F_B` is the output force on cylinder B

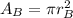`A_B=\pi r_B^2` is the surface area of cylinder B

Here we know that:

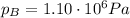`p_B=1.10\cdot 10^6 Pa` is the pressure

`r_B=2 in = 5.08 cm = 0.0508 m` is the radius, so the surface area is

`A_B=\pi r_B^2=\pi (0.0508)^2=8.11\cdot 10^(-3) m^2`

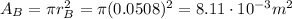
Therefore, the output force on cylinder B is:

`F_B=p_B A_B = (1.10\cdot 10^6 Pa)(8.11\cdot 10^(-3) m^2)=8918 N`

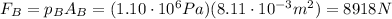
which corresponds to

`F_B=(8918 N)/(4.45)=2000 lb`