Question

Nu is designing a rectangular sandbox.The bottomm is 16 square feet.Which dimensions require the least amount of materail for the sides of the sand box?

Answer 1

Given Information:

Area of rectangle = 16 square feet

Required Information:

Least amount of material = ?

Answer:

x = 4 ft and y = 4 ft

Explanation:

We know that a rectangle has area = xy and perimeter = 2x + 2y

We want to use least amount of material to design the sandbox which means we want to minimize the perimeter which can be done by taking the derivative of perimeter and then setting it equal to 0.

So we have

xy = 16

y = 16/x

p = 2x + 2y

put the value of y into the equation of perimeter

p = 2x + 2(16/x)

p = 2x + 32/x

Take derivative with respect to x

d/dt (2x + 32/x)

2 - 32/x²

set the derivative equal to zero to minimize the perimeter

2 - 32/x² = 0

32/x² = 2

x² = 32/2

x² = 16

x =
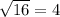`√(16) = 4` ft

put the value of x into equation xy = 16

(4)y = 16

y = 16/4

y = 4 ft

So the dimensions are x = 4 ft and y = 4 ft in order to use least amount of material.

Verification:

xy = 16

4*4 = 16

16 = 16 (satisfied)