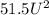Question

) An engineer deploys a set of sensors. Each sensor reports its location as a point in two-dimensional space. The points are (2, 7), (8, 2), (6, 11), (6, 5), and (11, 6). Use determinants to calculate the area of the polygon formed by the sensors.

Answer 1

The polygon area is
`51.5 U^(2)`

Explanation:

Points:

(2,7), (8,2), (6,11), (6,5), (11,6)

1. The area of the polygon could be calculate with the eqation:

`A=(1)/(2)\left[\begin{array}{ccc}x_(1) &y_(1)\\x_(2) &y_(2)\\x_(3) &y_(3)\\x_(4) &y_(4)\\x_(5) &y_(5)\end{array}\right]`

2. Replace the coordinates in equation for A:

`A=(1)/(2)\left[\begin{array}{ccc}2&7}\\8&2\\6&11\\6&5\\11&6\end{array}\right]`

3. Solve the determinant, and calculate A:

`A=(1)/(2)\left[\begin{array}{ccc}2&7}\\8&2\\6&11\\6&5\\11&6\end{array}\right]\\A=(1)/(2)[(6)(7)+(11)(11)+(8)(6)+(6)(2)]-[(2)(11)+(6)(6)+(11)(2)+(8)(5)]\\A=(1)/(2)[42+121+48+12]-[22+36+22+40]\\A=(1)/(2)[223]-[120]\\\\A=(1)/(2)[103]=51,5 U^(2)`

The polygon area is
`51.5 U^(2)`