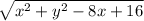 and mod(y-3)
and mod(y-3)
Explanation:
Step 1 :
Given the focus is at (4,0) and the directrix is y = 3. We have to find the 2 equations which relate the distance of the given focus and the given directrix to any point (x, y) on the parabola
Step 2 :
The distance between a point P(x,y) given on the parabola and the focus (4,0)
is
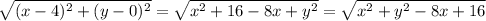
Step 3 :
The distance between the point P of (x,y) and the directrix line y = 3 is
mod (y-3)
So the 2 required equations are
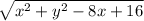 and mod(y-3)
and mod(y-3)