Answer:
One triangle
Explanation:
step 1
Find the measure of side AC
In the right triangle of the left
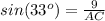 ----> by SOH (opposite side divided by the hypotenuse)
----> by SOH (opposite side divided by the hypotenuse)
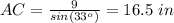
step 2
Find the measure of angle B
Applying the law of sines

substitute the given values

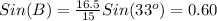
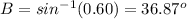
step 3
Find the measure of angle C
Remember that the sum of the interior angles of a triangle must be equal to 180 degrees
so
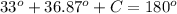
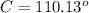
step 4
Find the measure of side AB
Applying the law of sines
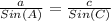
substitute the given values
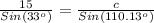
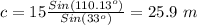
Each measure of the ABC triangle can only have one value, therefore only one triangle can be make with the given measures