Answer:
a) Therefore, the probability is P=0.98.
b) Therefore, the probability is P=0.02.
c) Therefore, the probability is P=0.72.
d) Therefore, the probability is P=0.18.
Explanation:
We know that: One type has a reliability of 0.9; that is, the probability that it will activate the sprinkler when it should is 0.9.
The other type, which operates independently of the first type, has a reliability of 0.8.
We get
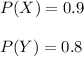
a) We calculate the probability that the sprinkler head will be activated.
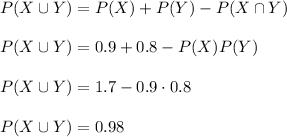
Therefore, the probability is P=0.98.
b) We calculate the probability that the sprinkler head will not be activated.
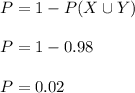
Therefore, the probability is P=0.02.
c) We calculate the probability that both activation devices will work properly.
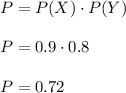
Therefore, the probability is P=0.72.
d) We calculate the probability that only the device with reliability 0.9 will work properly.
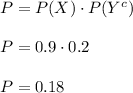
Therefore, the probability is P=0.18.