Question

The coordinates of quadrilateral ABCD are A(-1,-5), B(8,2), C(11,13), and D(2,6). Using coordinate geometry, prove that quadrilateral ABCD is a rhombus

Answer 1

The quadrilateral ABCD is a rhombus.

Explanation:

A rhombus is a quadrilateral having equal sides.

If ABCD is a rhombus then,

AB = BC = CD = DA

It is provided that the coordinates of the rhombus ABCD are:

A = (-1, -5)

B = (8, 2)

C = (11, 13)

D = (2, 6)

Use the distance formula to compute the lengths of AB, BC, CD and DA.

The distance formula is:

`d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

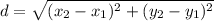
Compute the length of AB:

`AB=\sqrt{(8-(-1))^(2)+(2-(-5))^(2)}=√(130)=11.4`

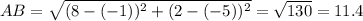
Compute the length of BC:

`BC=\sqrt{(11-8)^(2)+(13-2)^(2)}=√(130)=11.4`

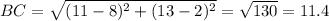
Compute the length of CD:

`CD=\sqrt{(2-11)^(2)+(6-13)^(2)}=√(130)=11.4`

Compute the length of DA:

`DA=\sqrt{(2-(-1))^(2)+(6-(-5))^(2)}=√(130)=11.4`

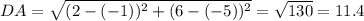
Thus, the lengths AB, BC, CD and DA are equal, i.e. all sides are of length 11.4.

Hence proved that the quadrilateral ABCD is a rhombus.