Question

A decomposition reaction has a half life of 578 years. (a) What is the rate constant for this reaction? (b) How many years does it take for the reactant concentration to reach 12.5% of its original value? Report your answer to 3 significant figures.

Answer 1

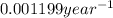`0.001199 year^(-1)` is the rate constant for this reaction.

It will take
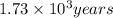`1.73* 10^3 years` to concentration to reach 12.5% of its original value.

Step-by-step explanation:

A decomposition reaction follows first order kinetics:

Half life of the reaction =
`t_(1/2)=578 years`

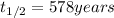
Rate constant of the reaction = k

For first order reaction, half life and rate constant are linked with an expression :

`k=(0.693)/(t_(1/2))`

`k=(0.693)/(578 years)=0.001199 year^(-1)`

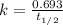
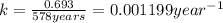
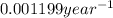`0.001199 year^(-1)` is the rate constant for this reaction.

Initial concentration of reactant =
`[A_o]` = x

Final concentration of reactant after time t =
`[A]` = 12.5% of x = 0.125x

The integrated law of first order reaction :

`[A]=[A_o]* e^(-kt)`

`0.125x=x* e^{-0.001199 year^(-1)* t}`

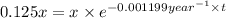
t = 1,734.31 years =
`1.73* 10^3 years`

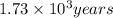
It will take
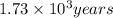`1.73* 10^3 years` to concentration to reach 12.5% of its original value.