Question

A certain type of plywood consists of six layers. The thickness of the layers are independent and normally distributed with mean 5mm and standard deviation 0.2mm.a) Find the mean thickness of the plywood and the standard deviation.b) Find the probability that the plywood is less than 28 mm thick

Answer 1

a.) The mean of the six layered plywood is 30 mm

The standard deviation is 0.49 mm

b.) That the thickness is less than 28 mm has a probability of 0.000022.

Explanation:

There are six layers in a plywood that is considered. It is also given that the layers are independent and normally distributed.

The thickness of the layers of the plywood have a mean,
`\mu` = 5 mm

and a standard deviation,
`\sigma` = 0.2 mm.

a.) Therefore the mean of the six layered plywood is = 6
`\mu`

= 6 × 5 mmm

= 30 mm

The standard deviation of the six layered plywood =
`\sqrt{6 \sigma^(2) }` =
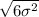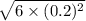`√(6 * (0.2)^2)` = 0.49 mm

b.) We are given to find that the probability of the plywood is less than 28 mm thick.

P( thickness < 28 mm)

P( Z <
`((28 - 30))/(0.49)`) = P(Z <
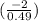`((-2)/(0.49) )`) ⇒ P( Z < -4.082) = 0.000022