Question

A manufacturer produces bearings, but because of variability in the production process, not all of the bearings have the same diameter. The diameters have a normal distribution with a mean of 1.3 centimeters (cm) and a standard deviation of 0.01 cm. The manufacturer has determined that diameters in the range of 1.27 to 1.33 cm are acceptable. What proportion of all bearings falls in the acceptable range?

Answer 1

Proportion of all bearings falls in the acceptable range = 0.9973 or 99.73% .

Explanation:

We are given that the diameters have a normal distribution with a mean of 1.3 centimeters (cm) and a standard deviation of 0.01 cm i.e.;

Mean,
`\mu` = 1.3 cm and Standard deviation,
`\sigma` = 0.01 cm

Also, since distribution is normal;

Z =
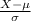`(X -\mu)/(\sigma)` ~ N(0,1)

Let X = range of diameters

So, P(1.27 < X < 1.33) = P(X < 1.33) - P(X <=1.27)

P(X < 1.33) = P(
`(X -\mu)/(\sigma)` <
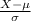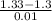`(1.33 -1.3)/(0.01)` ) = P(Z < 3) = 0.99865

P(X <= 1.27) = P(
`(X -\mu)/(\sigma)` <
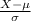`(1.27 -1.3)/(0.01)` ) = P(Z < -3) = 1 - P(Z < 3) = 1 - 0.99865

= 0.00135

P(1.27 < X < 1.33) = 0.99865 - 0.00135 = 0.9973 .

Therefore, proportion of all bearings that falls in this acceptable range is 99.73% .