Question

Write the general equation for the circle that passes through the points (1, 1), (1, 3), and (9, 2).

You must include the appropriate sign (+ or -) in your answer. Do not use spaces in your answer.
8x² + 8y²___x___y = 0

Answer 1

The general equation for the circle that passes through the points (1, 1), (1, 3), and (9, 2) is:

`x^2+y^2 -9.6875x-2.5y + 7.1875 = 0`

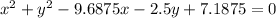
Solution:

Given that,

Write the general equation for the circle that passes through the points (1, 1), (1, 3), and (9, 2)

The general equation of the circle is of the form:

`x^(2) + y^(2) +2gx+2fy + c= 0`

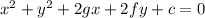
The circle passes through the point (1, 1)

Replacing x = 1 and y = 1 must satisfy the equation.

Using these values, we get:

`1^2 + 2^2 + 2g(1) + 2f(1) + c = 0\\\\1 + 4 + 2g + 2f + c = 0\\\\2g + 2f + c = -5 --------- eqn\ 1`

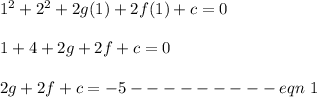
The circle passes through the point (1, 3)

Replacing x = 1 and y = 3 must satisfy the equation

`1^2 + 3^2+ 2g(1) + 2f(3) + c = 0\\\\1+9+2g + 6f + c = 0\\\\2g + 6f + c = -10 --------- eqn\ 2`

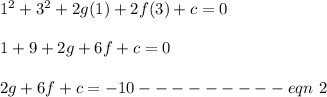
The circle passes through the point (9, 2)

Replacing x = 9 and y = 2 must satisfy the equation

`9^2 + 2^2 + 2g(9) + 2f(2) + c = 0\\\\81 + 4 + 18g + 4f + c = 0\\\\18g + 4f + c = -85 ---------- eqn\ 3`

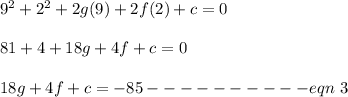
Solving eqn 1, 2, 3 using elimination, we get,

g = -4.84375

f = -1.25

c = 7.1875

Thus the general equation for the circle is:

Substitute the g, f, c values in general equation

`x^2+y^2+2(-4.84375)x +2y(-1.25) +7.1875 = 0\\\\x^2+y^2 -9.6875x-2.5y + 7.1875 = 0`

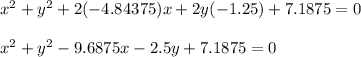
Thus the general equation for the circle is found