Explanation:
- The square root of a product of two positive real numbers is the product of their square roots.
Let 4 and 5 be the two positive real number. The square root of a product of 4 and 5 is the product of their square roots.
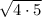
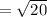
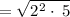
![\mathrm{Apply\:radical\:rule}:\quad \sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/g6m7j3nxcetkydzl367nxmff8yjwxx8ng4.png)
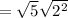
so
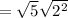
![\mathrm{Apply\:radical\:rule}:\quad \sqrt[n]{a^n}=a](https://img.qammunity.org/2021/formulas/mathematics/middle-school/i4rotrku70hayfwz0yf6jqsuylpf6j3wti.png)
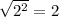
Therefore,
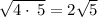
NOW SOLVING BY APPLYING RADICAL RULE such that
![\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/r95b2r0faczrvp3mlf77v9s1oj4nkg4akj.png)
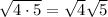
as
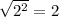
so
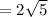
Hence, The square root of a product of two positive real numbers is the product of their square roots.