Assuming you're asking "for which values of
 the function
the function
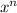 has an inverse that is a function", the answer is "all the odd exponents
has an inverse that is a function", the answer is "all the odd exponents
 ".
".
Infact, if
 is even, you have that
is even, you have that
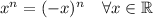
and so
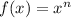 is not injective, and thus not invertible
is not injective, and thus not invertible
On the other hand, if
 is odd, we have:
is odd, we have:
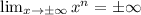
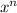 is continuous.
is continuous.- The first two points tell us that the function is surjective.
- Moreover, the derivative is
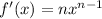 . Since
. Since
 is even, we have
is even, we have
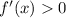 , thus the function is always increasing, and so the function is also injective.
, thus the function is always increasing, and so the function is also injective. - Injective and surjective means bijective, and the function can be inverted.