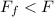Question

An automobile with a tangential speed of 54.1 km/h follows a circular road that has a radius of 41.6 m. The automobile has a mass of 1260 kg. The pavement is wet and oily, so the coefficient of kinetic friction between the car's tires and the pavement is only 0.500.

Answer 1

1) Available force of friction: 6174 N

2) No

Step-by-step explanation:

1)

The magnitude of the frictional force between the car's tires and the pavement of the road is given by

`F_f=\mu mg`

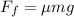
where

`\mu` is the coefficient of friction

m is the mass of the car

g is the acceleration of gravity

For the car in this problem, we have:

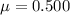`\mu=0.500` (coefficient of friction)

m = 1260 kg (mass of the car)

`g=9.8 m/s^2`

Therefore, the force of friction is

`F_f=(0.500)(1260)(9.8)=6174 N`

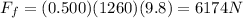
2)

In order to mantain the car in circular motion, the force of friction must be at least equal to the centripetal force.

The centripetal force is given by

`F=m(v^2)/(r)`

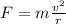
where

m is the mass of the car

v is the tangential speed

r is the radius of the curve

In this problem, we have

m = 1260 kg

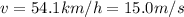`v=54.1 km/h =15.0 m/s` is the tangential speed

r = 41.6 m is the radius of the curve

Therefore, the centripetal force is

`F=(1260)(15.0^2)/(41.6)=6814 N`

Therefore, the force of friction is not enough to keep the car in the curve, since
`F_f<F`