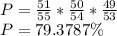Question

A local fraternity is conducting a raffle where 55 tickets are to be sold—one per customer. There are three prizes to be awarded. If the four organizers of the raffle each buy one ticket, what are the following probabilities? (Round your answers to five decimal places.) (a) What is the probability that the four organizers win all of the prizes? (b) What is the probability that the four organizers win exactly two of the prizes? (c) What is the probability that the four organizers win exactly one of the prizes? (d) What is the probability that the four organizers win none of the prizes?

Answer 1

(a) 0.0152%

(b) 1.1663%

(c) 19.4297%

(d) 79.3787%

Explanation:

Tickets bought by organizers = 4

Number of tickets = 55

Prizes = 3

(a) The probability that the four organizers win all of the prizes is:

`P = (4)/(55)*(3)/(54)*(2)/(53)\\P=0.0152\%`

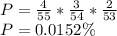
(b) The probability that the four organizers win exactly two of the prizes is:

`P = (4)/(55)*(3)/(54)*(51)/(53)+(4)/(55)*(51)/(54)*(3)/(53)+(51)/(55)*(4)/(54)*(3)/(53)\\P=1.1663\%`

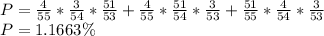
(c) The probability that the four organizers win exactly one of the prizes is:

`P = (4)/(55)*(51)/(54)*(50)/(53)+(51)/(55)*(4)/(54)*(50)/(53)+(51)/(55)*(50)/(54)*(4)/(53)\\P=19.4397\%`

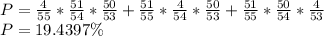
(d) The probability that the four organizers win none of the prizes is:

`P = (51)/(55)*(50)/(54)*(49)/(53)}\\P=79.3787\%`