Answer:
5.579 *
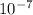 or 0.00005579 %
or 0.00005579 %
Explanation:
In this question, you select 11 random adults, so the order is not important and we should use combination instead of permutation. There are two different probability here
A= chance that the adults need correction= 0.81
B= chance that the adult doesn't need correction = 0.19
The case that can fulfill the condition of no more than 1 of 11 adults need correction is:
1. 0 adult need correction = 0C11 *

2. 1 adult need correction = 1C11 *
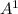 *
*
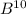
Then the probability will be:
0C11 *
 +1C11 *
+1C11 *
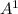 *
*
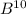 =
=
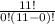 *
*
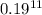 +
+
 *
*
 *0.81 =
*0.81 =
5.579 *
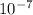 = 0.00005579 %
= 0.00005579 %
The threshold for a significant value that widely used is 5% and the chance is lower than 5%, so no more than 1 adult need correction is a significantly low number of adults requiring eyesight correction?