Answer:
The gate will open if the height of water is equal to or more than 0.337m.
Step-by-step explanation:
From the diagram attached, (as seen from the reference question found on google)
The forces are given as
Force on OA
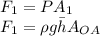
Here
- ρ is the density of water.
- g is the gravitational acceleration constant
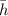 is the equivalent height given as
is the equivalent height given as
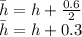
 is the area of the OA part of the door which is calculated as follows:
is the area of the OA part of the door which is calculated as follows:
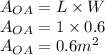
The Force is given as
![F_1=0.6\rho g[h+0.3]](https://img.qammunity.org/2021/formulas/physics/college/oxe0242dken4w9ak32n52ulpfkt5q8m8jc.png)
Force on OB
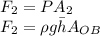
Here
- ρ is the density of water.
- g is the gravitational acceleration constant
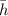 is the equivalent height given as
is the equivalent height given as
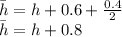
 is the area of the OB part of the door which is calculated as follows:
is the area of the OB part of the door which is calculated as follows:
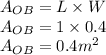
The Force is given as
![F_2=0.4\rho g[h+0.8]](https://img.qammunity.org/2021/formulas/physics/college/tsya5dh5pd9rzxkao6rq77tbpacfux32xb.png)
Now the moment arms are given as
![\bar{y}_a=\bar{h}+\frac{I}{A\bar{h}}\\\bar{y}_a=h+0.3+((1)/(12)* 0.6^3 * 1)/(0.6 *[h+0.3])\\\bar{y}_a=h+0.3+(0.03)/(h+0.3)](https://img.qammunity.org/2021/formulas/physics/college/s58ukml7yf9bmgwgrkcr3vv8g6z96wgvn2.png)
![\bar{y}_b=\bar{h}+\frac{I}{A\bar{h}}\\\bar{y}_b=h+0.8+((1)/(12)* 0.4^3 * 1)/(0.4 *[h+0.8])\\\bar{y}_b=h+0.8+(0.0133)/(h+0.8)](https://img.qammunity.org/2021/formulas/physics/college/kc1igmsv9dpzsxafotuvli1wadruhlps2u.png)
Taking moment about the point O as zero
/(h+0.3))=0.4\rho g[h+0.8](0.2+(0.0133)/(h+0.8))\\0.6[h+0.3](0.3-(0.03)/(h+0.3))=0.4[h+0.8](0.2+(0.0133)/(h+0.8))\\0.18h -0.054-0.018=0.08h+0.064+0.00533\\h=0.337 m](https://img.qammunity.org/2021/formulas/physics/college/7eufjrosq9b6ler8fo23ng1lfqbyr8ggwv.png)
So the gate will open if the height of water is equal to or more than 0.337m.