Answer:
a =
 . Surface Area =
. Surface Area =

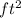 . and area of the Dish =
. and area of the Dish =

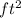 +pi
+pi
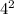 =
=

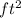 +50.27=51.6
+50.27=51.6
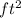
Explanation:
(1) Constant. y(x) = a
 that is the curve that we need to rotate around the y axis to get the parabola with diameter of 8 feet and 2 meter depth that statement is translated in mathematics as x = -4 to 4 and y = 0 to 2.
that is the curve that we need to rotate around the y axis to get the parabola with diameter of 8 feet and 2 meter depth that statement is translated in mathematics as x = -4 to 4 and y = 0 to 2.
y max = 2, x max = 4 setting up a equation with a unknown gives
2=a4 and a =
 .
.
so we have now.
y(x) =
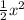 (Done with solving for a Constant).
(Done with solving for a Constant).
(2) Surface Area.
Setting Up surface integral.
(i) range in x = 0 to 4.
(ii) range in y = 0 to 2.
integral is.
Integral(0-2)[{integral[(0-4)
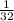
 ]}]dy
]}]dy
Evaluating this integral gives.

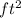 .
.
and area is surface area + area of the circle with 8ft diameter.
=

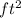 +pi
+pi
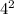 =
=

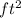 +50.27=51.6
+50.27=51.6
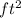 ...
...
Note the Difference between area and aurface area.!