Question

Need help with this problem

Answer 1

Shown in image

Explanation:

Graph of the Secant Function

The secant function is the reciprocal of the cosine function, that means:

`\displaystyle f(x)=secx=(1)/(cosx)`

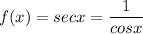
There are some statements posed about the secant function, let's find out which of them are true

The secant has infinite vertical asymptotes, one for each time the cosine is 0. To find out the points, we only need to solve

`cosx=0`

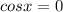
The cosine is zero at

`\displaystyle x=(\pi)/(2),\ (3\pi)/(2)`

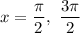
in the first rotation. We must check those two options among the correct answers

Now, we evaluate

`\displaystyle sec(\pi)/(4)=(1)/(cos(\pi)/(4))=(1)/((√(2))/(2))=√(2)`

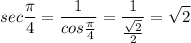
Let's compute now

`\displaystyle sec(\pi)/(3)=(1)/(cos(\pi)/(3))=(1)/((1)/(2))=2`

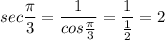
All the correct options are shown in the attached image