Question

Suppose that grade point averages of undergraduate students at one university have a bell-shaped distribution with a mean of 2.62 and a standard deviation of 0.39. Using the empirical rule, what percentage of the students have grade point averages that are at least 3.4? Please do not round your answer.

Answer 1

• 97.5% of the students have grade point averages that are at least 3.4

Step-by-step explanation:

1. Find how many standard deviations is 3.4 from the mean, 2.62

`z-score=\frac{x-mean}{standard\text{ }deviation}`

`z-score=(3.4-2.62)/0.39=2`

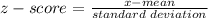
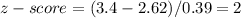
2. Apply the empirical rule

The empirical rule, or 68 - 95 - 99.7 rule, states that, for a normal distribution (a bell-shaped distribution), 68% of the data are within one standar deviation of the mean, 95% of the data are within two standard deviations from the mean, and 99.7% of the data are within three standard deviations from the mean.

We calculated that 3.4 is 2 standard deviations from the mean.

Since 95% of the data are within 2 standard deviations from the mean, 5% of the data are out of the 2 standard deviations region; half of that (2.5%) are abovethe mean + 2 standard deviations

Hence, the grade point averages of 95% + 2.5% of the students are below the mean plus two standard deviations, and you can say that that is the percentage of students whose grade point averages are at least 3.4.

• 95% + 2.5% = 97.5%