A survey of Amazon.com shoppers reveals the following probability distribution of the number of books purchased per hit. X 0 1 2 3 4 5 6 7 P(X) .35 .25 .20 .08 .06 .03 .02 .01 a…

Question

asked Dec 1, 2021 166k views

1 Answer

Alexpotato · Answer 1 · 2021-12-08T13:44:45+0000

Answer:

a)
P(X=4) = 0.06

b)
P(X=8) = 0

c)
P(X=0) = 0.35

d)
$P(X\geq 1)= 1-P(X<1) = 1-P(X=0) = 1-0.35 =0.65$

Explanation:

For this case we define the random variable X as "number of books purchased per hit."

And as we can see the distribution for x is given by:

X 0 1 2 3 4 5 6 7

P(X) .35 .25 .20 .08 .06 .03 .02 .01

Part a

For this case we want this probability:

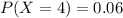P(X=4) = 0.06 from the probability distribution given

Part b

For this case we want this probability:

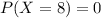P(X=8) = 0 from the probability distribution given since the value of X=8 is not in the distribution

Part c

For this case we want this probability:

P(X=0) = 0.35 from the probability distribution given

Part d

For this case we want this probability:

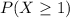
$P(X\geq 1)$

And we can use the complement rule like this:

$P(X\geq 1)= 1-P(X<1) = 1-P(X=0) = 1-0.35 =0.65$