Answer: 0.01
Explanation:
Let the events are :
C = paving stones found to be cracked.
D = paving stones found to be discolored.
Given : Total stones : T = 600 (i)
C = 15
D= 27
C'∩D'= 564 (ii)
Since C'∩D' = (C∪D)' = T- C∪D (iii)
From (i) , (ii)and (ii) , we have
564 = 600- C∪D
⇒ C∪D=600- 564= 36
Formula : C∩D= C+D- C∪D
Put values , we get
C∩D= 15+27-36=6
Now ,
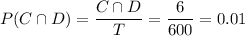
The probability that it is both cracked and distorted is 0.01.