Answer:
The magnitude of the force that one of the particles exerts on the other is F = 1.4026 x
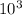 N
N
Step-by-step explanation:
Using Coulomb's law which states that "the force of attraction or repulsion between two charged particles is directly proportional to the product of the magnitude of their charges and inversely proportional to the square of the distance separating these particles".
Mathematically;
F = k x
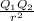
Where;
k = Coulomb's constant = 9 x
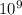 N
N
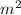 /
/
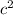
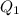 = Charge on first particle = - 4.61 μC = - 4.61 x
= Charge on first particle = - 4.61 μC = - 4.61 x
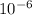 C (You may ignore the sign. The sign is just showing that the particle is negatively charged)
C (You may ignore the sign. The sign is just showing that the particle is negatively charged)
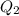 = Charge on second particle = 6.07 μC = 6.07 x
= Charge on second particle = 6.07 μC = 6.07 x
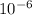 C
C
r = distance between the two particles = 1.34cm = 0.0134m = 1.34 x
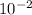 m
m
Substituting these values into the equation above gives;
F = 9 x
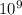 x 4.61 x
x 4.61 x
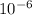 x 6.07 x
x 6.07 x
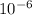 ÷
÷
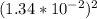
Solve the equation;
F = 9 x 4.61 x 6.07 x
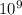 x
x
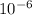 x
x
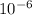 ÷ (1.34 x 1.34 x
÷ (1.34 x 1.34 x
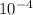 )
)
F = 9 x 4.61 x 6.07 x
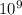 x
x
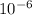 x
x
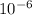 x
x
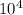 ÷ (1.34 x 1.34)
÷ (1.34 x 1.34)
F = 251.8443 x 10 ÷ 1.7956
F = 140.26 x 10
F = 1.4026 x
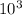 N
N
Therefore the magnitude of the force that one of the particles exerts on the other is F = 1.4026 x
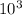 N
N