Question

4. For a series of experimentally measured values give the definition of (a) average or mean value (b) the deviation from the mean (c) average deviation (d) standard deviation 5. Explain how one can express experimental result using the quantities discussed in (4).

Answer 1

a) x_average = ∑
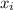`x_(i)` / n , b) Δx_{i} = x_{i} –x_average,

d) σ = √(1/n-1 ∑ Dx_{i}² )

Step-by-step explanation:

Some definitions are requested

a) the average value is the sum of all the values ​​divided by the number of them, if the uncertainties are random, this is the closest value to the real one

x_average = ∑
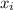`x_(i)` / n

b) The deviation from the mean value or absolute error is the measured value minus the average value

Δx_{i} = x_{i} –x_average

c) is the average value of the deviations

Δx_average = ∑ Δx_{i} / n

d) It is a measure of the dispersion of the values ​​with respect to their average value, it takes the worst of all cases, widely used for large numbers of data

σ = √(1/n-1 ∑ Dx_{i}² )

Experimental results should be given as follows

Average value ± uncertainty and the standard deviation

(x_average + - Δx_average)

σ