Question

She sights two sailboats going due east from the tower. The angles of depression to the two boats are 42o and 29o. If the observation deck is 1,353 feet high, how far apart are the boats?

Answer 1

The boats are 934.65 feet apart

Step-by-step explanation:

Given:

The angles of depression to the two boats are 42 degrees and 29 degrees

Height of the observation deck i = 1,353 feet

To Find:

How far apart are the boats (y )= ?

Solution:

Step 1 : Finding the value of x(Refer the figure attached)

We can use the tangent ratio to find the x value

`tan(42^(\circ)) = (1353)/(x)`

`x = (1353)/(tan(42^(\circ)) )`

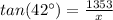
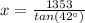
x = 590.47 feet

Step 2 : Finding the value of z (Refer the figure attached)

`tan(29^(\circ)) = (1353)/(z )`

`z = (1353)/(tan(29^(\circ)))`

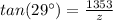
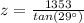
z = 1525.12 feet

Step 3 : Finding the value of y (Refer the figure attached)

y = z -x

y = 1525.12 - 590.47

y = 934.65 feet

Thus the two boats are 934.65 feet apart