Question

Which binomial is a factor of 49x^2+84xy+36y^2

Answer 1

7x + 6y is a binomial that is a factor of given equation

Solution:

A binomial is a mathematical expression which has only two terms

Given expression is:

`49x^2 + 84xy + 36y^2`

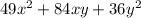
We have to find the binomial that is a factor to given expression

Let us find the factors of given equation

`49x^2+84xy+36y^2\\\\\mathrm{Rewrite\:}49x^2+84xy+36y^2\mathrm{\:as\:}\left(7x\right)^2+2\cdot \:7x\cdot \:6y+\left(6y\right)^2\\\\\mathrm{Rewrite\:}49\mathrm{\:as\:}7^2\\\\7^2x^2+84xy+36y^2\\\\\mathrm{Rewrite\:}36\mathrm{\:as\:}6^2\\\\7^2x^2+84xy+6^2y^2\\\\\mathrm{Apply\:exponent\:rule}:\quad \:a^mb^m=\left(ab\right)^m\\\\7^2x^2=\left(7x\right)^2\\\\Therefore,\\\\\left(7x\right)^2+84xy+6^2y^2\\\\\mathrm{Apply\:exponent\:rule}:\quad \:a^mb^m=\left(ab\right)^m\\\\6^2y^2=\left(6y\right)^2\\\\`

`Therefore\\\\\left(7x\right)^2+84xy+\left(6y\right)^2\\\\\mathrm{Rewrite\:}84xy\mathrm{\:as\:}2\cdot \:7x\cdot \:6y\\\\\left(7x\right)^2+2\cdot \:7x\cdot \:6y+\left(6y\right)^2\\\\\left(7x\right)^2+2\cdot \:7x\cdot \:6y+\left(6y\right)^2\\\\`

`\mathrm{Apply\:Perfect\:Square\:Formula}:\quad \left(a+b\right)^2=a^2+2ab+b^2\\\\a=7x,\:b=6y\\\\Therefore,\\\\\left(7x\right)^2+2\cdot \:7x\cdot \:6y+\left(6y\right)^2 = \left(7x+6y\right)^2`

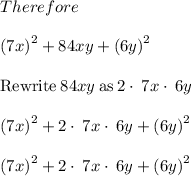
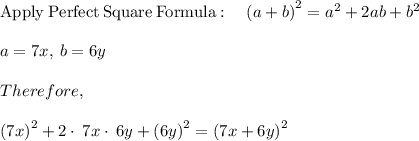
Thus we get,

`49x^2 + 84xy + 36y^2 = (7x+6y)^2\\\\49x^2 + 84xy + 36y^2 = (7x+6y)(7x+6y)`

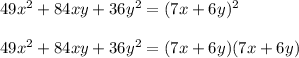
Thus the binomial which is a factor is 7x + 6y