Question

Please Help!!!

What is a polynomial function in standard form with zeroes 1, 2, -3, and -1 ?

Answer 1

`p(x) = {x}^(4) + {x}^(3) - 7 {x}^(2) - x + 6`

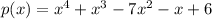
Explanation:

The polynomial function has zeros

x=1, x=2,x=-3,x=-1

This means the factored form of the polynomial is

`p(x) = (x - 1)(x + 1)(x + 3)(x - 2)`

We expand to get:

`p(x) = ( {x}^(2) - 1)( {x}^(2) + x - 6)`

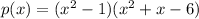
We expand further to get:

`p(x) = {x}^(2)( {x}^(2) + x - 6) - 1({x}^(2) + x - 6)`

`p(x) = {x}^(4) + {x}^(3) - 6 {x}^(2) - {x}^(2) - x + 6`

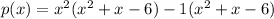
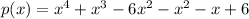
This simplifies to:

`p(x) = {x}^(4) + {x}^(3) - 7 {x}^(2) - x + 6`

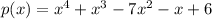
This is the standard form of the polynomial since it is written in descending powers of x.