Question

How do I use the cosine rule for these problems?

Answer 1

see explanation

Explanation:

Using the Cosine rule

a² = b² + c² - 2abcosA ← Rearranging for cosA gives

cosA =
`(b^2+c^2-a^2)/(2ab)`

(a)

let a = 10, b = 7, c = 8 and A = α, then

cosα =
`(7^2+8^2-10^2)/(2(7)(8))` =
`(49+64-100)/(112)` =
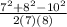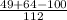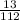`(13)/(112)`, thus

α =
`cos^(-1)`(
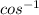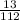`(13)/(112)` ) ≈ 83° ( to the nearest degree )

(b)

let the angle opposite side 7 be x

Using the Sine rule

`(10)/(sin83)` =
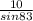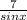`(7)/(sinx)` ( cross- multiply )

10sinx = 7sin83 ( divide both sides by 10 )

sinx =
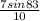`(7sin83)/(10)` , thus

x =
`sin^(-1)` (
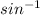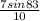`(7sin83)/(10)` ) = 44°

The third angle can be found using the sum of angles in a triangle

third angle = 180° - (83 + 44)° = 180° - 127° = 53°

The 3 angles are 83°, 44°, 53°