Question

3. Using techniques from Calculus, show directly that the maximum value of a 1-D Gaussian distribution occurs at the point x = μ.

Answer 1

For a scaler variable, the Gaussian distribution has a probability density function of

p(x |µ, σ² ) = N(x; µ, σ² ) = 1 / 2π×
`e^{(-(x-u)^(2))/(2s^(2) ) }`

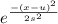
The term will have a maximum value at the top of the slope of the 1-D Gaussian distribution curve that is when exp(0) =1 or when x = µ

Explanation:

Gaussian distributions have similar shape, with the mean controlling the location and the variance controls the dispersion

From the graph of the probability distribution function it is seen that the the peak is the point at which the slope = 0, where µ = 0 and σ² = 1 then solution for the peak = exponential function = 0 or x = µ