Question

A tank contains 90 kg of salt and 1000 L of water. A solution of a concentration 0.045 kg of salt per liter enters a tank at the rate 8 L/min. The solution is mixed and drains from the tank at the same rate.a) What is the concentration of the solution in the tank initially?

b) Find the amount of salt in the tank after 4 hours.
c) Find the concentration of salt in the solution in the tank as time approaches infinity.

Answer 1

Explanation:

concentration = amount of salt/solution

A) Initial concentration= 90/1000 = 0.09

Q = quantity of salt

Q(0) = 90 kg

Inflow rate = 8 l/min

Outflow rate = 8 l/min

Solution = 1000 L at any time t.

Salt inflow = 0.045 * 8 per minute

= 0.36 kg per minute

This is mixed and drains from the tank.

Outflow =
`(Q(t))/(1000)`

Thus rate of change of salt

Q'(t) = inflow - outflow =
`0.36-(Q(t))/(1000) \\=(360-Q(t))/(1000)`

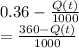
Separate the variables and integrate

`(1000dQ)/(360-q(t)) =dt\\-1000 ln |360-Q(t)| = t+C\\ln |360-Q(t)| = -0.001+C'\\360-Q(t) = Ae^(-0.001t) \\Q(t) = 360-Ae^(-0.001t)`

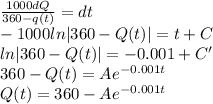
Use the fact that Q(0) = 90

90 = 360-A

A = 270

So

`Q(t) = 360-270e^(-0.001t)`

B) Q(t) = 360-270e^-0.004 = 91.07784

C) When t approaches infinity, we get

Q(t) tends to 360

So concentration =360/1000 = 0.36