Question

Which set of ordered pairs has point symmetry with respect to the origin (0, 0)?

(-8, 3), (8, -3)
(-8, 3), (-3, 8)
(-8, 3), (-8, -3)
(-8, 3), (8, 3)

Answer 1

(-8, 3), (8, -3)

Explanation:

I copied the other dude

Answer 2

(-8, 3), (8, -3)

Explanation:

Point symmetry about origin means reflection of the given point about the origin.

The reflection of a point about the origin will cause the 'x' and 'y' value of the point to change its sign.

Therefore, the coordinate rule for point symmetry about the origin is given as:

`(x,y)\to (-x,-y)`

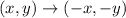
Now, let us check each of the given options.

Option 1:

(-8, 3), (8, -3)

Now, if (x, y) = (-8, 3), then its point symmetry is given as (-(-8), -3) = (8, -3)

So, option 1 is correct.

Option 2:

(-8, 3), (-3, 8)

Now, if (x, y) = (-8, 3), then its point symmetry is given as (-(-8), -3) = (8, -3) ≠ (-3, 8)

So, option 2 is not correct.

Option 3:

(-8, 3), (-8, -3)

Now, if (x, y) = (-8, 3), then its point symmetry is given as (-(-8), -3) = (8, -3) ≠ (-8, -3)

So, option 3 is not correct.

Option 4:

(-8, 3), (8, 3)

Now, if (x, y) = (-8, 3), then its point symmetry is given as (-(-8), -3) = (8, -3) ≠ (8, 3)

So, option 4 is not correct.

Hence, only option 1 is correct.