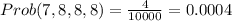Question

In a state lottery, four digits are drawn at random one at a time with replacement from 0 to 9. Suppose that you win if any permutation of your selected inte- gers is drawn. Give the probability of winning if you select.(a) 6, 7, 8, 9. (b) 6, 7, 8, 8. (c) 7, 7, 8, 8. (d) 7, 8, 8, 8.

Answer 1

(a) 0.0024

(b) 0.0012

(c) 0.0006

(d) 0.0004

Explanation:

The total number of possible integers when any number is selected is 10 (i.e from 0 - 9). When four number integers are selected, the total number of sample sample will be;

10 × 10 × 10 × 10 = 10,000

The sample space = 10,000

To know the possible ways of selecting the given four digits, we will use permutation.

`^(n)P_(r) = (n!)/((n-r)!)`

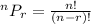
To get the probability,

`Probability \ of \ winning (Selected \ numbers) = (number\ of\ possible\ outcomes\ of\ selected\ numbers)/(sample\ space)`

(a) When 6,7,8,9 are selected, n = 4 , r = 4

The possible ways of selecting 6,7,8,9 is;

`^(4)P_(4) = (4!)/((4-4)!)`

`= (4!)/((0)!)`

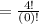
but 0! = 1

`^(4)P_(4) = 4!`

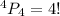
= 4 × 3 × 2 × 1 = 24

`Prob (6,7,8,9) = (24)/(10000) = 0.0024`

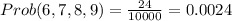
(b) When 6, 7, 8, 8 are selected,

The possible ways of selecting 6,7,8,8 is;

`= (4!)/(1! \ 1! \ 2!)`

`= (4!)/(2!)`

`=(4 * 3 * 2 * 1)/(2 * 1)`

= 12

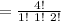
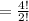
`Prob (6,7,8,8) = (12)/(10000) = 0.0012`

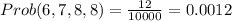
(c) When 7, 7, 8, 8 are selected,

The possible ways of selecting 7,7,8,8 is;

`= (4!)/(2! \ 2!)`

`=(4 * 3 * 2 * 1)/((2 * 1)(2 * 1))`

= 6

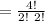
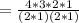
`Prob (7,7,8,8) = (6)/(10000) = 0.0006`

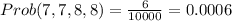
(d) When 7, 8, 8, 8 are selected,

The possible ways of selecting 7,8,8,8 is;

`= (4!)/(1! \ 3!)`

`=(4 * 3 * 2 * 1)/(3 * 2 * 1)`

= 4

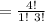
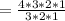
`Prob (7,8,8,8) = (4)/(10000) = 0.0004`