Question

If Alex and Brandon work together, they will finish cleaning the school in 15 hours. Working alone, Brandon can finish the same job in 20 hours. How long will it take Alex to do the job by himself?

Answer 1

Alex can do the job in 60 days alone.

Explanation:

Alex and Brandon working together, they can finish the job of cleaning the school in 15 hours. Brandon alone in 20 hours can finish the job.

So, Brandon can complete
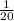`(1)/(20)` part of the job in one hour.

Let, Alex alone can finish the same job in x hours.

So, Alex can complete
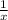`(1)/(x)` part of the job in one hour.

So, working together they do
`((1)/(20) + (1)/(x)) = (x + 20)/(20x)` part of the whole job in one hour.

Hence, from the conditions given we can write

`(x + 20)/(20x) = (1)/(15)`

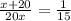
⇒ 15x + 300 = 20x

⇒ 5x = 300

⇒ x = 60 days.

Therefore, Alex can do the job in 60 days alone. (Answer)