Question

Complete the square to write the quadratic expression in vertex form.

All incorrect or incomplete answers will be reported. Please show all work.

Answer 1

1. (x - 3)² = 8

2. (x + 2)² = 3

3. (x + 6)² =
`$ (101)/(2) $`

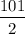
4. (x + 3)² = 27

5. (x + 4)² = 13

6.
`$ \bigg( x - (15)/(9) \bigg) ^2 = (261)/(81) = (29)/(9) $`

Explanation:

Completion of Square:
`$ (x - a) ^2 = x^2 - 2ax + a^2 $`

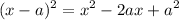
In the following problems the terms in the RHS of the above equation may be missing. We balance the equation. Simplify it and re write it in terms of LHS.

1. x² - 6x + 1 = 0

Taking the constant term to the other side, we get:

x² - 6x = - 1

⇒ x² - 2(3)x = -1

⇒ x² -2(3)x + 9 = - 1 + 9 [Adding 9 to both the sides]

⇒ x² -2(3)x + 3² = 8

⇒ (x - 3)² = 8 is the answer.

2. 3x² + 12x + 3 = 0

Note that the co-effecient of x² is not 1. We make it 1, by dividing the whole equation by 3. And then proceed like the previous problem.

3x² + 12x = -3

Dividing by 3 through out, x² + 4x = - 1

⇒ x² + 2(2) + 4 = -1 + 4

⇒ x² +2(2) + 2² = 3

⇒ (x + 2)² = 3 is the answer.

3. 2x² + 24x = 29

x² + 12x =
`$ (29)/(2) $`

⇒ x² + 2(6)x + 36 =
`$ (29)/(2) $` + 36

⇒ x² + 2(6)x + 6² =
`$ (29 + 72)/(2) $`

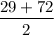
⇒ (x + 6)² =
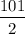`$ (101)/(2) $` is the answer.

4. x² + 6x - 18 = 0

x² + 6x = 18

⇒ x² + 2(3)x = 18

⇒ x² + 2(3)x + 9 = 18 + 9

⇒ x² + 2(3)x + 3² = 27

⇒ (x + 3)² = 27 is the answer.

5. x² + 8x + 3 = 0

x² + 8x = -3

⇒ x² + 2(4)x = -3

⇒ x² + 2(4)x + 16 = - 3 + 16

⇒ x² + 2(4)x + 16 = 13

⇒ (x + 4)² = 13 is the answer.

6. 9x² - 30x + 6 = 0

9x² - 30x = - 6

⇒ x²
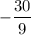`$ - (30)/(9) $` x = - 6

`$ \implies x^2 -2 \bigg( (15)/(9) \bigg )x + (225)/(81) = - 6 + (225)/(81) $`

`$ \implies x^2 - 2\bigg( (15)/(9) \bigg ) x + \bigg ( (15)/(9) \bigg ) ^2 = (261)/(81) $`

`$ \bigg( x - (15)/(9) \bigg) ^2 = (261)/(81) = (29)/(9) $` is the answer.