Question

Caleb invested $80,000 in an account paying an interest rate of 5.4% compounded monthly. Assuming no deposits or withdrawals are made, how much money, to the nearest ten dollars, would be in the account after 13 years?

Answer 1

`\large \boxed{\text{\$161 170}}`

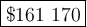
Explanation:

The formula for the amount (A) accrued on an investment earning compound interest is

`A = P(1 + (r)/(n))^(nt)`

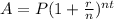
where

P = the amount of money invested (the principal)

r = the annual interest rate expressed as a decimal fraction

t = the time in years

n = the number of compounding periods per year

Data:

P = $80 000

r = 5.4 % = 0.054

t = 13 yr

n = 12 /yr

Calculation:

`\begin{array}{rcl}A& =& P \left (1 + (r)/(n) \right )^(nt)\\& =& 80000 \left(1 + (0.054)/(12) \right )^(12*13)\\\\& =& 80000 (1 + 0.0045 )^(156)\\& =& 80000 (1.0045)^(156)\\& =& 80000 * 2.01461\\& =& \mathbf{161170}\\\end{array}\\\text{The account would contain $\large \boxed{\textbf{\$161 170}}$}`