Question

A top-loading washing machine has a cylindrical basket that rotates about a vertical axis. The basket of one such machine starts from rest and reaches an angular speed of 3.0 rev/s in 7.0 s. The lid of the machine is then opened, which turns off the machine, and the basket slows to rest in 14.0 s. Through how many revolutions does the basket turn during this 21 s interval? Assume constant angular acceleration while it is starting and stopping.

Answer 1

32 revolutions

Step-by-step explanation:

t = Time taken

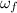`\omega_f` = Final angular velocity

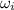`\omega_i` = Initial angular velocity

`\alpha` = Angular acceleration

`\theta` = Number of rotation

Equation of rotational motion

`\omega_f=\omega_i+\alpha t\\\Rightarrow \alpha=(\omega_f-\omega_i)/(t)\\\Rightarrow \alpha=(3-0)/(7)\\\Rightarrow \alpha=0.42857142857\ rev/s^2`

`\omega_f^2-\omega_i^2=2\alpha \theta\\\Rightarrow \theta=(\omega_f^2-\omega_i^2)/(2\alpha)\\\Rightarrow \theta=(3^2-0^2)/(2* 0.42857142857)\\\Rightarrow \theta=10.5\ rev`

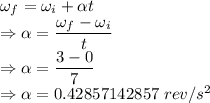
Number of revolutions in the 7 seconds is 10.5

`\omega_f=\omega_i+\alpha t\\\Rightarrow \alpha=(\omega_f-\omega_i)/(t)\\\Rightarrow \alpha=(0-3)/(14)\\\Rightarrow a=-0.214285714286\ rev/s^2`

`\omega_f^2-\omega_i^2=2\alpha \theta\\\Rightarrow \theta=(\omega_f^2-\omega_i^2)/(2\alpha)\\\Rightarrow \theta=(0^2-3^2)/(2* -0.214285714286)\\\Rightarrow \theta=21\ rev`

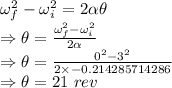
Number of revolutions in the 14 seconds is 21

Total total number of revolutions in the 20 second interval is 10.5+21 = 31.5 = 32 revolutions