Answer:
a)
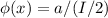
b)
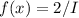
Explanation:
a) Lets denote
 the cumulative distribution function of X. Note that for any value a between 0 and I/2, we have that
the cumulative distribution function of X. Note that for any value a between 0 and I/2, we have that
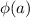 is the probability for the stick to be broken before the length a is reached following the stick from one starting point plus the probability for the stick to be broken after the length I-a from the same starting point. This means that
is the probability for the stick to be broken before the length a is reached following the stick from one starting point plus the probability for the stick to be broken after the length I-a from the same starting point. This means that

b) Note that, as a consecuence of what we calculate in the previous item, X has a uniform distribution with parameter I/2, therefore, the probability density function f is
f(x) = 1/(I/2) = 2/I