Question

The angular momentum of a flywheel having a rotational inertia of 0.200 kg · m2 about its central axis decreases from 3.80 to 0.600 kg · m2/s in 1.30 s

(b) Assuming a uniform angular acceleration, through what angle does the flywheel turn? (c) How much work is done on the wheel? (d) What is the average power of the flywheel?

Answer 1

14.3065 rad

-36.777 J

-28.29 W

Step-by-step explanation:

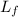`L_f` = Final angular momentum = 0.6 kgm²/s

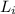`L_i` = Initial angular momentum = 3 kgm²/s

I = Moment of inertia = 0.2 kgm²

Torque is given by

`\tau=(L_f-L_i)/(t)\\\Rightarrow \tau=(0.6-3.8)/(1.3)\\\Rightarrow \tau=-2.46\ Nm`

`\theta=\omega_it+(1)/(2)\alpha t^2`

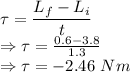
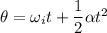
Initial angular speed is given by

`\omega_i=(L_i)/(I)`

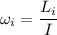
Angular acceleration is given by

`\alpha=(\tau)/(I)`

`\theta=\omega_it+(1)/(2)\alpha t^2\\\Rightarrow \theta=(L_it+(1)/(2)\tau t^2)/(I)\\\Rightarrow \theta=(3.8* 1.3+(1)/(2)* -2.46* 1.3^2)/(0.2)\\\Rightarrow \theta=14.3065\ rad`

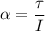
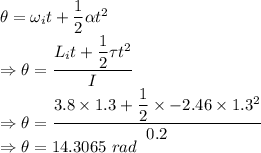
The angle is 14.3065 rad

Work done is given by

`W=\tau \theta\\\Rightarrow W=-2.46* 14.95\\\Rightarrow W=-36.777\ J`

The work done on the wheel is -36.777 J

Power is given by

`P=(W)/(t)\\\Rightarrow P=(-36.777)/(1.3)\\\Rightarrow P=-28.29\ W`

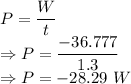
The power is -28.29 W