Question

Rectangle A has a length of 80 inches and a width of 30 inches. Rectangle A has the same area as Rectangle B, but has different dimensions. The width of Rectangle B is 80% shorter than the width of Rectangle A as shown. Which percent represents how much longer the length of Rectangle B must be to maintain the same area as Rectangle A?

Answer 1

The length of rectangle B must to be 25% greater than the length of rectangle A

Explanation:

step 1

Find the area of rectangle A

`A=LW`

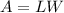
substitute the given values

`A=(80)(30)=2,400\ in^2`

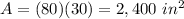
step 2

Find the width of rectangle B

Multiply by 0.80 (80%) the width of rectangle A

`W=0.80(30)=24\ in`

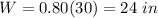
step 3

Find the length of rectangle B

we have

`A=2,400\ in^2\\W=24\ in`

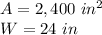
substitute in the formula of area

`A=LW`

`2,400=24L`

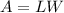
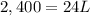
solve for L

`L=100\ in`

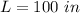
step 4

Find the percentage

we know that

The length of rectangle A represent 100%

so

using proportion

Find out what percentage represent the difference of its length

100-80=20 in

`(80)/(100\%)=(20)/(x)\\\\x=100(20)/80\\\\x=25\%`

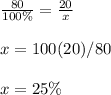
therefore

The length of rectangle B must to be 25% greater than the length of rectangle A