Question

Part of the analysis we routinely do with datasets is to identify whether or not any of the variables included are Binomial or Poisson in nature.

Discuss why it can be helpful to do this?

Answer 1

This is useful to choose which calculation to perform.

Explanation:

1) Firstly, let's consider that the Binomial Distribution tends to the Poisson Distribution given certain conditions:

`n\rightarrow \infty, p\rightarrow 0, \lambda =np`

Roughly, they tend to the same value.

2) The Binomial Probability is calculated through this formula:

`Binomial: P(X=x)=\binom{n}{x}p^(x)(1-p)^(n-x)`

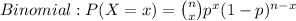
Poisson Distribution this way:

`Poisson:P(X=x)=(\lambda^(x) e^(-\lambda ))/(x!)`

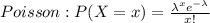
3) If we plug

`p=(\lambda )/(n)`

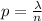
In the Binomial formula, given an "n" a very large quantity we'll have a closer outcome to Poisson.

`P(X=x)=\binom{n}{x}\left ( (\lambda )/(n) \right )^(x)(1-(\lambda )/(n))^(n-x) \approx (\lambda^(x) e^(-\lambda ))/(x!)`

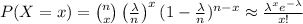
4) This is useful especially due to the convenience of calculating.

Because operating with exponentials and factorials, is hard and sometimes 'n' and 'p' may also be unknown, and sometimes the known parameter is the Mean.