Question

The sum of four numbers in arithmetic progression is 16. The square of the last number is the square of the first number plus 48. What are the four numbers?

Answer 1

four numbers are 1, 3, 5, 7

Explanation:

The sum of four numbers in arithmetic progression is 16

a, a+d, a+2d, a+3d are the four arithmetic series

sum of 4 numbers are

`a+a+d+a+2d+a+3d=4a+6d`

`4a+6d= 16`

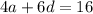
divide both sides by 2

`2a+3d=8`

`3d= 8-2a`

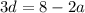
The square of the last number is the square of the first number plus 48.

`(a+3d)^2=a^2+48`

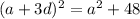
solve for a and d

`(a+3d)^2=a^2+48\\(a+8-2a)^2=a^2+48\\(8-a)^2=a^2+48\\a^2-16a+64=a^2+48\\-16a=48-64\\-16a=-16\\a=1`

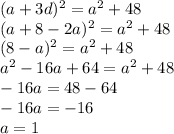
Now find out 'd'

`3d=8-2a\\3d=8-2\\3d=6\\a=2`

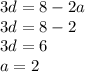
a, a+d, a+2d, a+3d

four numbers are 1, 3, 5, 7