Answer:
The margin of error is 3.97 percentage points.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence interval
, and a confidence interval
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
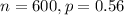
95% confidence interval
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
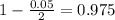 , so
, so
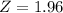 .
.
The lower limit of this interval is:
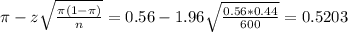
The upper limit of this interval is:
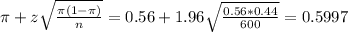
The margin of error is the upper limit subtracted by the proportion, or the proportion subtracted by the lower limit. They are the same values.
So the margin of error is 0.5997 - 0.56 = 0.56 - 0.5203 = 0.0397 = 3.97 percentage points.