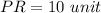Question

Find PR

PR = 2x
RQ = 25
PQ = 6+3x (adding 2 lengths as seen on diagram)​

Answer 1

Therefore,

`PR=10\ unit`

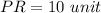
Explanation:

Given:

PR = 2x

RQ = 25

Say M divide PQ such that

PM = 6

MQ = 3x

∠PRM ≅ ∠QRM

RM is the angle Bisector of angle PRQ

To Find:

PR = ?

Solution:

Angle Bisector Theorem:

The angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle.

It equates their relative lengths to the relative lengths of the other two sides of the triangle.

Here RM is the angle Bisector of angle PRQ

Therefore,

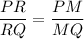`(PR)/(RQ)=(PM)/(MQ)` ...Angle Bisector Theorem.

Substituting the values we get

`(2x)/(25)=(6)/(3x)\\\\x^(2)=25\\Square\ Rooting\\x=\pm√(25)\\x=5`

As x cannot be negative x =5

Substituting x value in PR we get

`PR=2* 5=10\ unit`

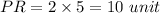
Therefore,

`PR=10\ unit`