Answer:
By examining the table of ordered pairs, notice that the function f(x) is the cube of
 . Therefore,
. Therefore,
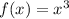
By examining the table of ordered pairs, notice that as
 increases by a constant value, the value of the function g(x) increases by the common ratio of 3. Therefore,
increases by a constant value, the value of the function g(x) increases by the common ratio of 3. Therefore,
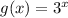
From the table, both functions equal 27 when
 , therefore, the point of intersection of the two functions is (3, 27).
, therefore, the point of intersection of the two functions is (3, 27).
As x increases past
 , g(x) increases quicker than f(x) since g(x) is an exponential function and f(x) is a cubic polynomial.
, g(x) increases quicker than f(x) since g(x) is an exponential function and f(x) is a cubic polynomial.
So the following statements are true:
- f(x) is a polynomial function
- g(x) is an exponential function
- The output values of g(x) will surpass those of f(x) as the input values continue to increase.
Please refer to the attached graph of both functions with plotted ordered pairs.