Question

Find all values of x such that (4, x, −6) and (2, x, x) are orthogonal. (Enter your answers as a comma-separated list.)

Answer 1

The values of x that make the vectors (4, x, −6) and (2, x, x) orthogonal are x = 2 and x = 4, determined by setting their dot product to zero and factoring the resulting quadratic equation.

Step-by-step explanation:

To find all values of x such that the vectors (4, x, −6) and (2, x, x) are orthogonal, we need to perform the dot product of the vectors and set it equal to zero. Two vectors are orthogonal if their dot product is zero.

The dot product is calculated as follows:

• (4)(2) + (x)(x) + (−6)(x) = 0
• 8 + x² − 6x = 0
• x² − 6x + 8 = 0

Next, we factor the quadratic equation:

• (x − 2)(x − 4) = 0

Hence, the two values of x that make the vectors orthogonal are x = 2 and x = 4.

Answer 2

The values of x that makes these vectors orthogonal are x = 2 and x = 4.

Step-by-step explanation:

Orthogonal vectors

Suppose we have two vectors:

`v_(1) = (a,b,c)`

`v_(2) = (d,e,f)`

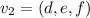
Their dot product is:

`(a,b,c).(d,e,f) = ad + be + cf`

They are ortogonal is their dot product is 0.

Solving quadratic equations:

To solve this problem, we are going to need tosolve a quadratic equation.

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

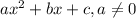This polynomial has roots
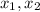`x_(1), x_(2)` such that
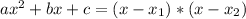`ax^(2) + bx + c = (x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4a`

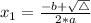
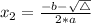
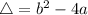
Find all values of x such that (4, x, −6) and (2, x, x) are orthogonal.

`(4,x,-6)(2,x,x) = 8 + x^(2) - 6x`

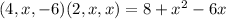
These vectors are going to be orthogonal if:

`x^(2) -6x + 8 = 0`

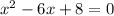
This is a quadratic equation, in which
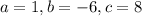`a = 1, b = -6, c = 8`. So

`\bigtriangleup = 6^(2) - 4*1*8 = 4`

`x_(1) = (-(-6) + √(4))/(2) = 4`

`x_(2) = (-(-6) - √(4))/(2) = 2`

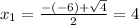
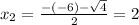
The values of x that makes these vectors orthogonal are x = 2 and x = 4.